

Q-Learning.md
Try the Frozen Lake Game

Conditional Common Entropy for Instrumental Variable Testing and Partial Identification
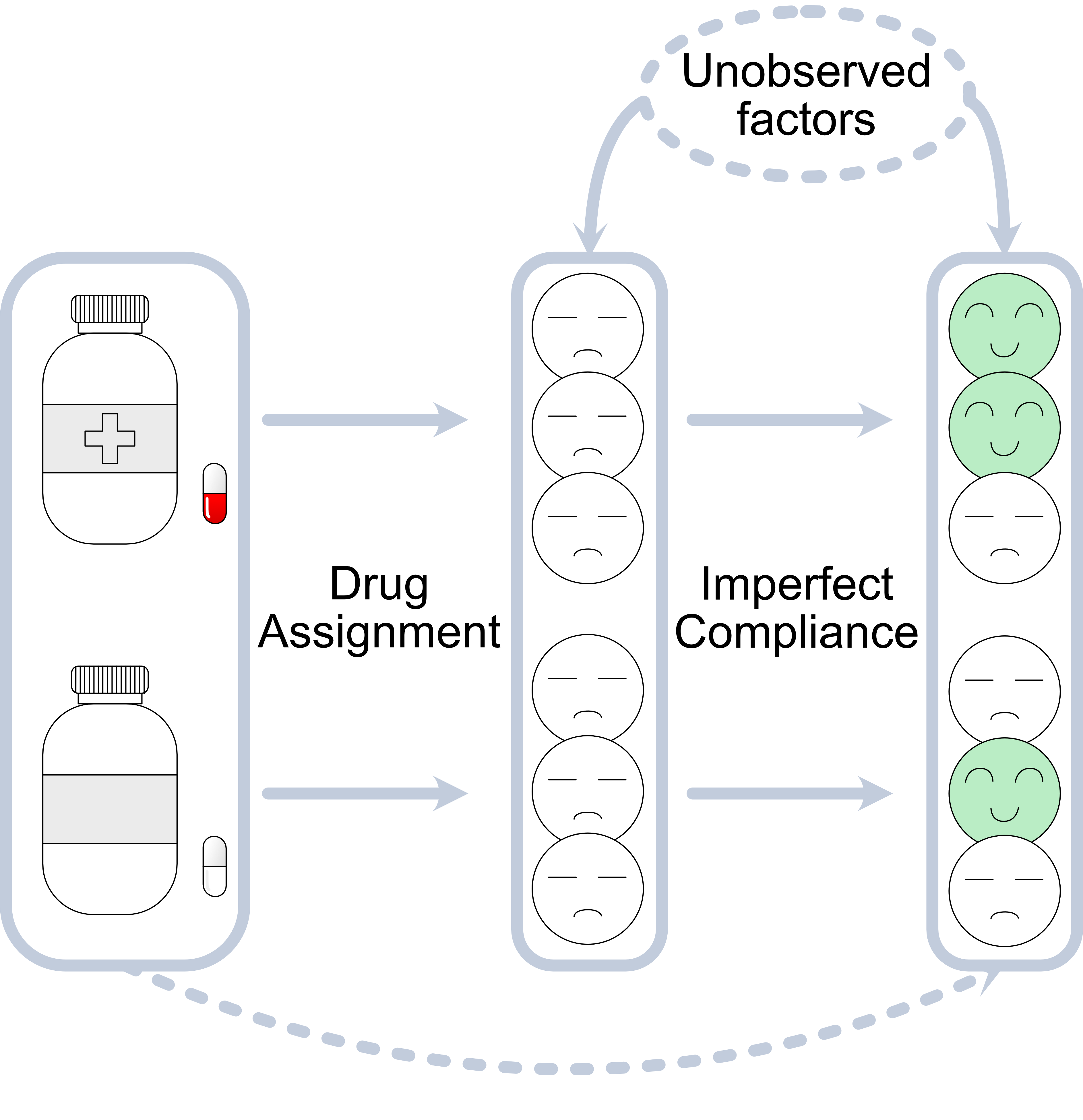
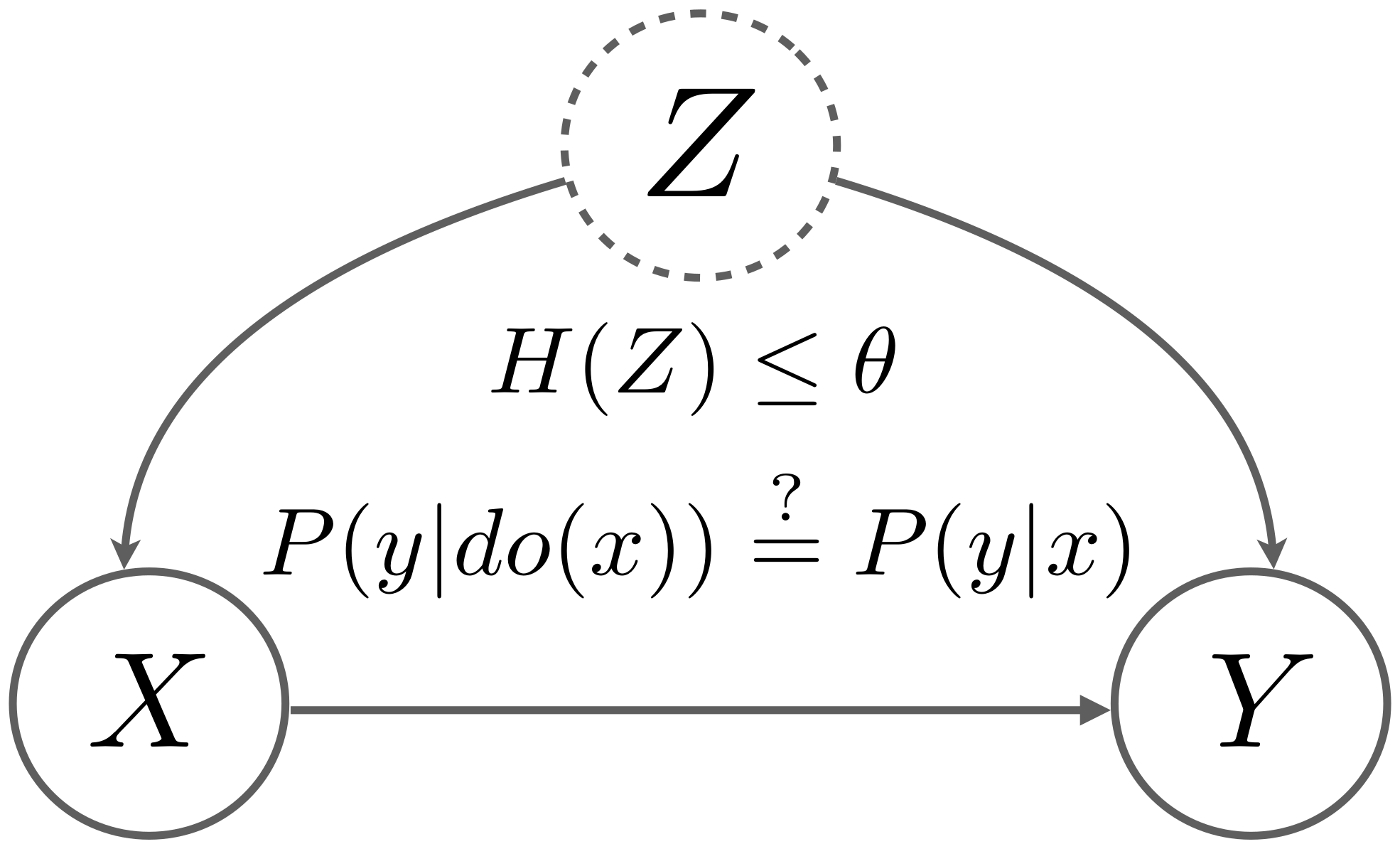
Overview Instrumental variables (IVs) are widely used for estimating causal effects. There are two main challenges when using instrumental variables. First of all, using IV without additional assumptions such as linearity, the causal effect may still not be identifiable. Second, when selecting an IV, the validity of the selected IV is typically not testable since the causal graph is not identifiable from observational data. In this work, we propose a method for bounding the causal effect with instrumental variables under weak confounding. In addition, we present a novel criterion to falsify the IV with side information about the confounder. ...
Approximate Causal Effect Identification under Weak Confounding
Overview In this project, we aimed to investigate the relationship between the influence of unobserved confounders and the deviation of spurious correlation from the true causal effect. This is similar to the concept of sensitivity analysis in the causal effect estimation. We utilized entropy as a measure to quantify the strength of the confounder and developed an algorithm to estimate bounds for the causal effect based on the observational distribution and the strength of confounders. ...
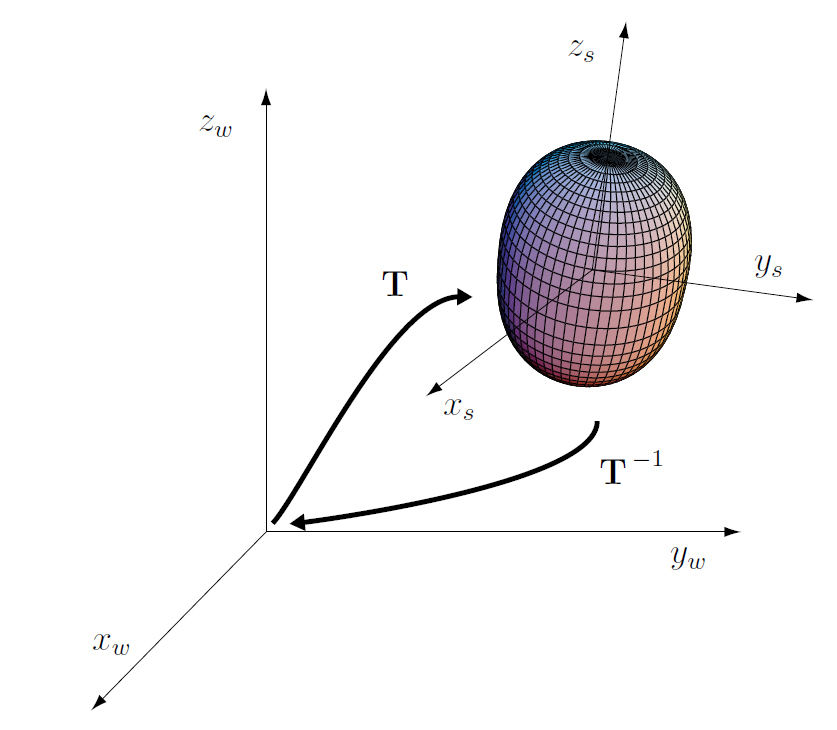
Extended Superquadric
Superquadric modeling was my first project in grad school, back when there were not as many 3D modeling techniques available as there are today. Using parametric models to describe 3D shapes has several advantages. First, this is a robust and efficient way to represent and recover 3D models for applications like large-scale building modeling. Second, the parametric model provides a natural way to describe shapes as primitives for applications such as point cloud segmentation and robot grasping. We used a variation called extended superquadric by Lin and Kambhamettu (2001) for the project. It involves some concepts in computational graphics, one without such background might need some time to grasp the idea. So I hope this post could be helpful as introductory material summarizing key points about the extended superquadric. ...
Robotics Specialization: Estimation and Learning
Here’s the content from the Robotics Specialization: Estimation and Learning offered by UPenn on Coursera. This is the fifth course in the robotics specialization. This course is about topics related to machine learning and estimation in robotics. Gaussian Model Learning 1D Gaussian Distribution The Gaussian distribution is a widely used probability distribution defined by two parameters, the mean (μ) and standard deviation (σ), which represent its central value and spread. It is characterized by a bell-shaped probability density function (PDF) and has some nice mathematical properties such as the product of two Gaussian distributions is also Gaussian. Additionally, the Central Limit Theorem states that the sum or average of a large number of independent and identically distributed random variables converges to a Gaussian distribution, making it suitable for modeling noise in measurement or uncertainty. ...
Robotics Specialization: Perception
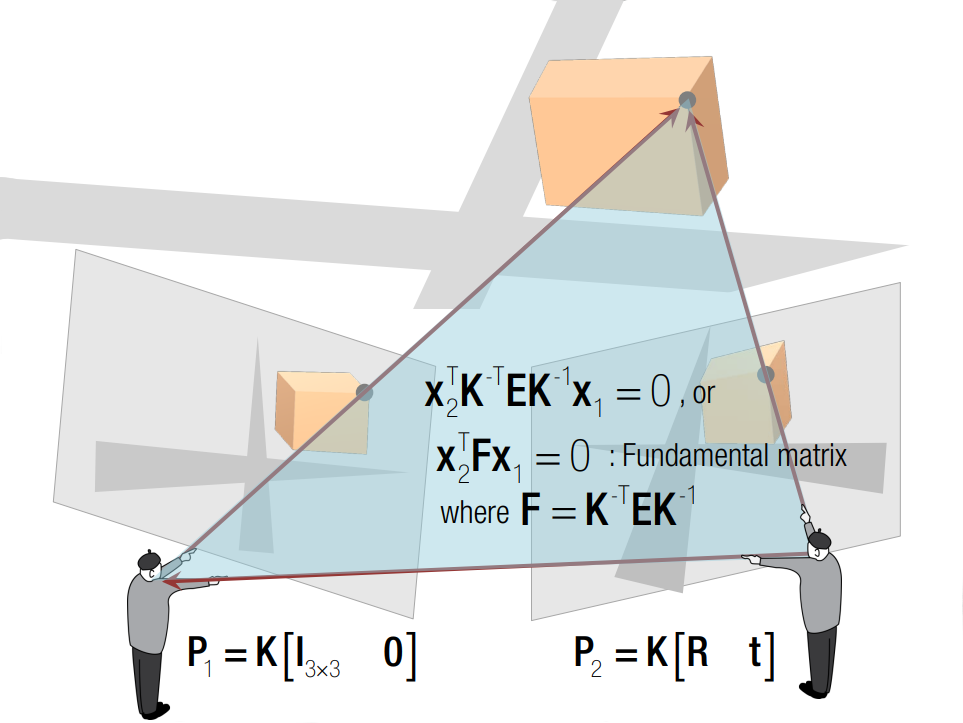
Here’s the content from the Robotics Specialization: Perception offered by UPenn on Coursera. This is the fourth course in the robotics specialization. Throughout this course, we learn the basics of computer vision that involve robotics. Single-view Geometry Pinhole Camera Pinhole camera The pinhole camera is the most commonly used camera model for computer vision. It can be seen as a simple form of perspective projection as shown in the figure below, which refers to the way objects in a three-dimensional scene appear on a two-dimensional surface when viewed from a particular point or viewpoint. The image below shows a 2D example. The rays from an object converge to some points in the image plane. Here $Y$ is the height of the object in the scene and $y$ is the height of the object in the image plane, $Z$ is the distance of the object from the camera, and $f$ is the focal length. ...
Robotics Specialization: Computational Motion Planning
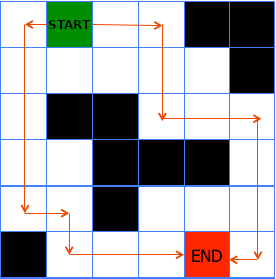
Here are the assignments for the Robotics Specialization: Computational Motion Planning offered by UPenn on Coursera. This is the second course in the robotics specialization. Throughout this course, we have gained knowledge on different techniques for planning robot motions. These include graph-based methods, randomized planners, and artificial potential fields. Graph-based Methods Graph-based methods tackle the challenge of planning routes for robots in environments with discrete positions, such as grids. To address this problem, we can represent such scenarios as graphs, where nodes signify grid locations, and edges indicate the routes between neighboring grid cells. In this course, we learned and implemented two graph-based algorithms, Dijkstra and the A-Star algorithm. ...
Robotics Specialization: Aerial Robotics
Here are the assignments for the Robotics Specialization: Aerial Robotics offered by UPenn on Coursera. In this course, we learned some basic ideas about autonomous robots and the design of quadrotors. There are three assignments in this course in which we learned to design a PD controller for a quadrotor in 1D, 2D, and 3D. The course provided quadrotor simulators to help with the experiment. The simulator uses MATLAB’s ODE solver, ode45, to simulate the behavior of the quadrotor and plt3 to visualize the state of the quadrotor at each time step. ...
