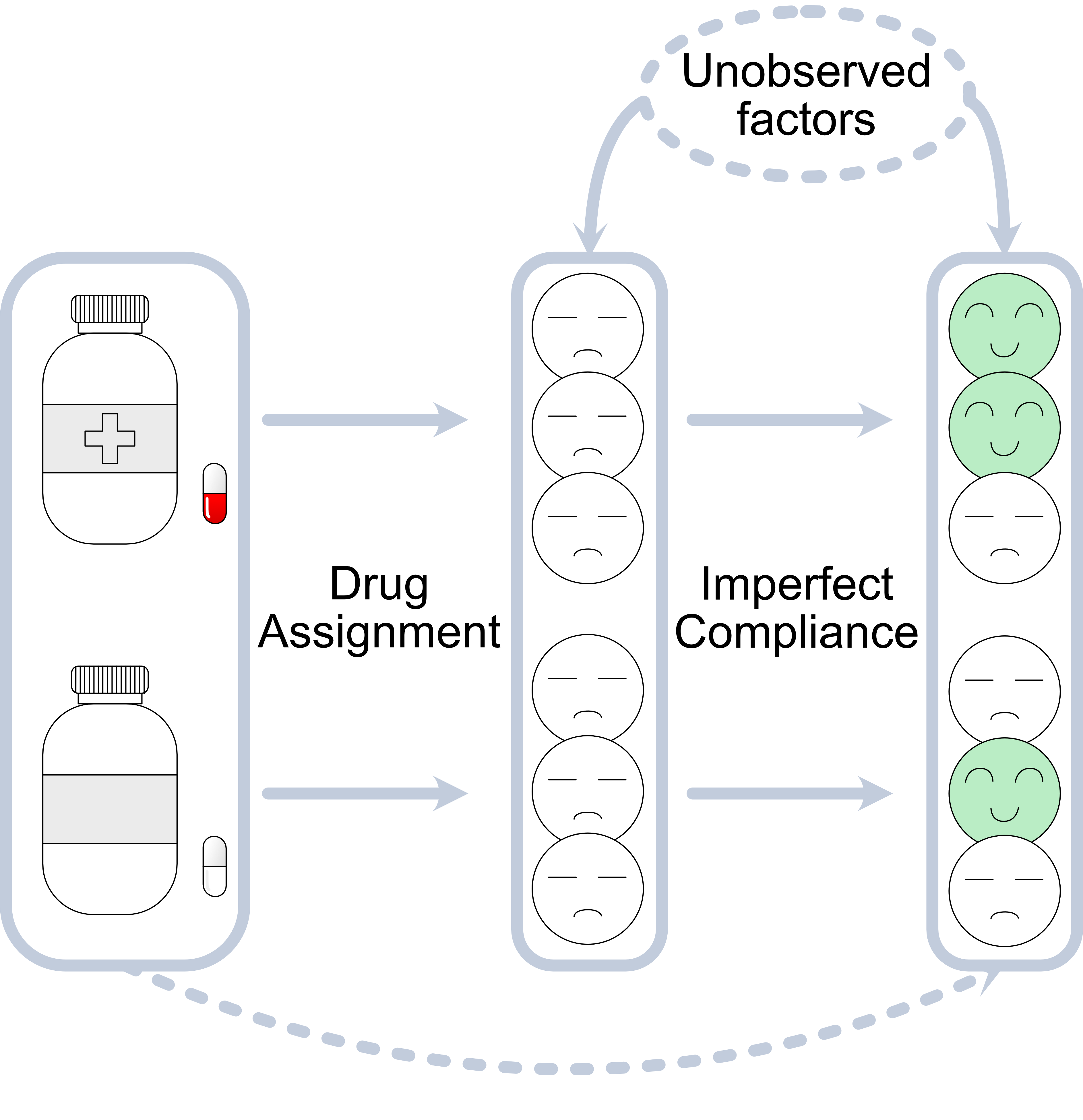
Overview
Instrumental variables (IVs) are widely used for estimating causal effects. There are two main challenges when using instrumental variables. First of all, using IV without additional assumptions such as linearity, the causal effect may still not be identifiable. Second, when selecting an IV, the validity of the selected IV is typically not testable since the causal graph is not identifiable from observational data. In this work, we propose a method for bounding the causal effect with instrumental variables under weak confounding. In addition, we present a novel criterion to falsify the IV with side information about the confounder.
Checkout Our Paper and Codes
Conditional Common Entropy for Instrumental Variable Testing and Partial Identification [code] Published in International Conference on Machine Learning (ICML), 2024
Instrumental Variable
Instrumental variable can be used to estimate the causal effect with observational data or in the inperfect compliance randomized experiments. The variable $Z$ is said to be an instrumental variable if (1) $Z$ is not independent of treatment variable $X$ (relevence), (2) $Z$ affects outcome variable $Y$ only through $X$ (exclusion), and (3) $Z$ is independent of the unobserved confounder (exchangeability). The last two assumptions are in general untestable since there is no conditional independence condition between $Z$ and $Y$ in the observational data. Under different assumption, instrumental vairables can be used to estimate the causal effect or the bounds of causal effects. In this paper, we focus on the following two assumptions.
Marginal stochastic exclusion $$E[Y_{z,x}] = E[Y_{z’,x}]\;\; \forall z,z’,x$$
Marginal exchangeability $$ Z \perp\!\!\!\!\perp Y_{z,x}\;\; \forall z,x $$
Under the above assumptions, the causal effect can be bounded by a closed-form expression, known as the natural bounds. The gap between bounds depends on the incompliance rate, so in some cases, the bounds of causal effects might be uninformative. Another challenge is that the assumption for instrumental variable is untestable. There exist some method to falsify the invalid instruments, but in general, one cannot confirm an instrumental varibale. So it is an interesting question about how to apply extra knowledge about the data to further verify the instrumental variables.
In this work, we derive a method using the side information of the latent confounder to (1) reject invalid instruments, (2) get tighter bounds of causal effect, (3) set up a sensitivity parameter for the violation of instrumental variable.
Common Entropy
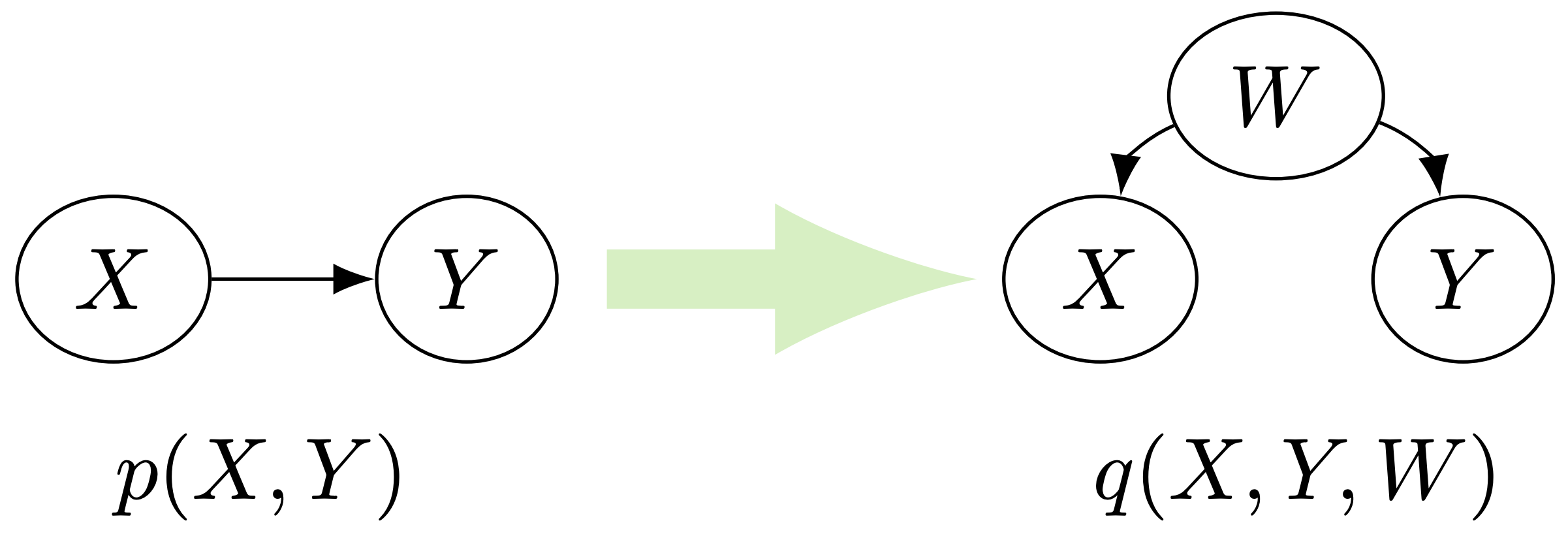
The exact common information was proposed by Kumar et al. (2014) to measure the common part of two random variables. Unlike mutual information, the exact common information measures the entropy of the simplest variable that explains the dependency between variables X and Y . This has also been referred to as the common entropy.
Formally, the common entropy is defined as
$$\begin{align*} \text{CE}(X;Y) &:= \min_{q(x,y,w)} H(W)\\ & \text{s.t. } I(X;Y|W) = 0; \\ & q(x,y,w) \text{ compatible with the obs} \end{align*} $$
$q(x,y,w)$ compatible with observed distribution means $$ \begin{align*} &\sum_w q(x,y,w) = p(x,y), \forall x,y; \\ & 0\leq q(x,y,w) \leq 1, \forall x,y,w \\ &\sum_{x,y,w} q(x,y,w) =1 .\nonumber \end{align*} $$
For a pair of variables $X,Y$ with joint distribution $P(X,Y)$, the common entropy is the minimum entropy $H(W)$ with joint distribution $P(X,Y,W)$ such that the joint distribution marginalize to $P(X,Y)$ and $X \perp\!\!\!\!\perp Y|W $.
Conditional Common Entropy
We extend the idea of common entropy to more general cases.
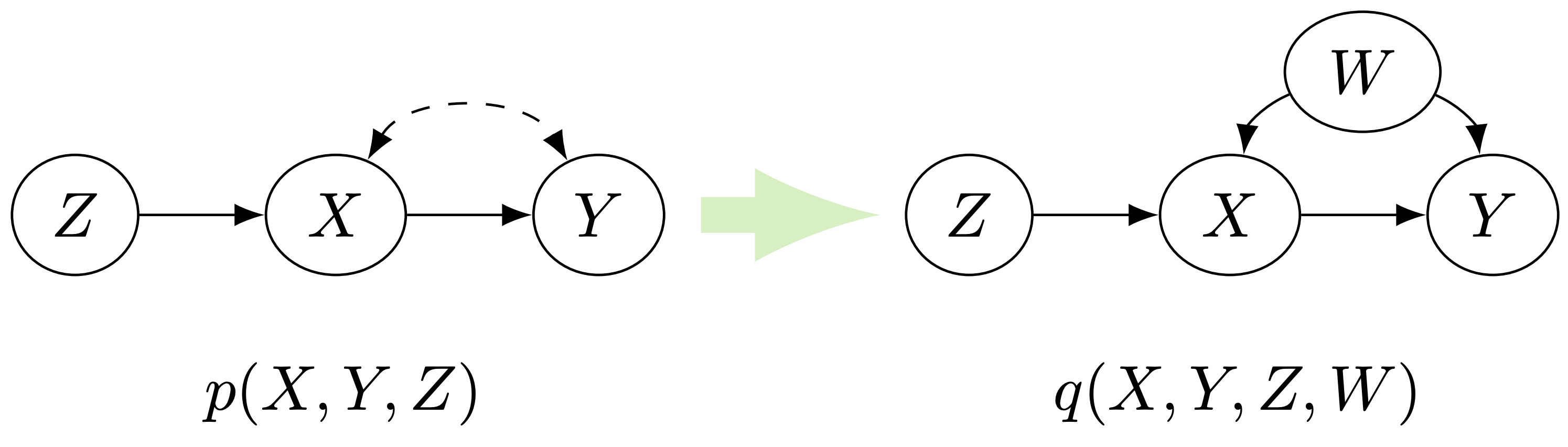
Conditional common entropy of two random variables $Z, Y$ given $X$ with the joint probability distribution $P(X, Y, Z)$ is defined as follows: $$ \begin{align*} CCE(Z;Y|X) &:= \min_{q(x,y,z,w)} H(W)\\ & \text{s.t. } I(Z;Y|X,W) = 0; \\ & q(x,y,z,w) \text{ compatible with the obs} \end{align*} $$
Then we developed the graph-specific conditional common entropy that can be used as a proxy for an edge strength.
Graph-Specific CCE
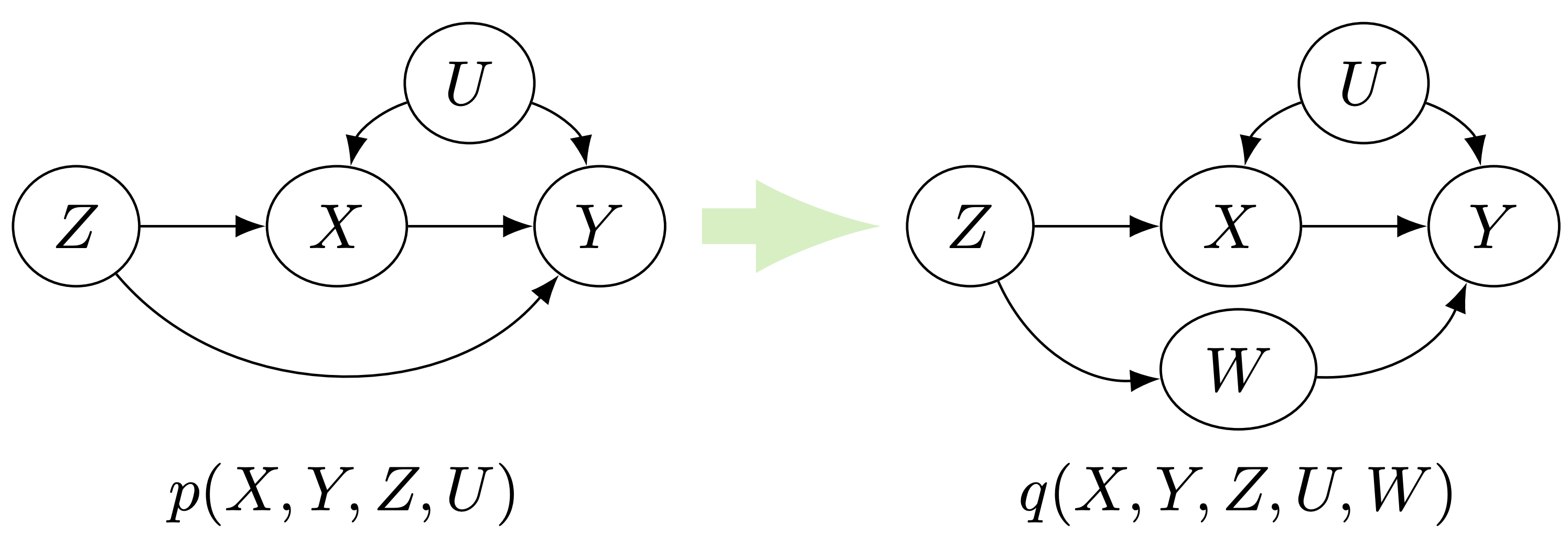
Let $P(\mathbf{V})$ be the joint distribution over variables $\mathbf{V}$ and Markov relative $\mathcal{G}$. Let $Z, Y\in \mathbf{V}$ satisfies $(Z\not\perp\!\!\!\!\perp_d Y|\mathbf{X})$ in $\mathcal{G}$ for a subset of variables $\mathbf{X}\subset\mathbf{V}$. Let $(v\leftrightarrow v’)$ or $(v\rightarrow v’)$ be an edge in $\mathcal{G}$ such that $(Z \perp\!\!\!\!\perp_d Y|\mathbf{X})$ upon its deletion. Define the \textbf{graph-specific conditional common entropy} $CCE_{\mathcal{G},(v\rightarrow v’)}$ to be the minimum entropy of $W$ for some $P(\mathbf{V}\cup {W})$ that compatible with the graph $\mathcal{G}’$, where $\mathcal{G}’ $ is the graph that replace $(v\rightarrow v’)$ with $(v\rightarrow W\rightarrow v’)$. Similarly define $CCE_{\mathcal{G},(v\leftrightarrow v’)}$ for $(v\leftrightarrow v’)$.
In words, the graph-specific conditional common entropy requires the variable $W$ to satisfies additional independence constraints according to the graph. For the IV graph, it requires the variable $W$ independent of the instrument $Z$. Therefore the $CCE_\mathcal{IV}$ is a lower bound for the entropy of latent confounders.
Similarly, if the confoudner between $X,Y$ is observed, we can also quantify the direct effect from $Z$ to $Y$.
Estimating the common entropy is NP-hard, so we propose the IV LatentSearch algorithm to approximate the graph-specific CCE.
First we relax the indepdent constraint to form the objective function $$ \mathcal{L} = I(Z;Y|X,W) +\beta_0 H(W) + \beta_1 I(W;Z).$$
The algorithm is as shown below.

By running the IV LatentSearch algorithm for different value of $\beta_0, \beta_1$, we get the varible $W$ with different entropy and different conditional mutual information as shown in the figure below.
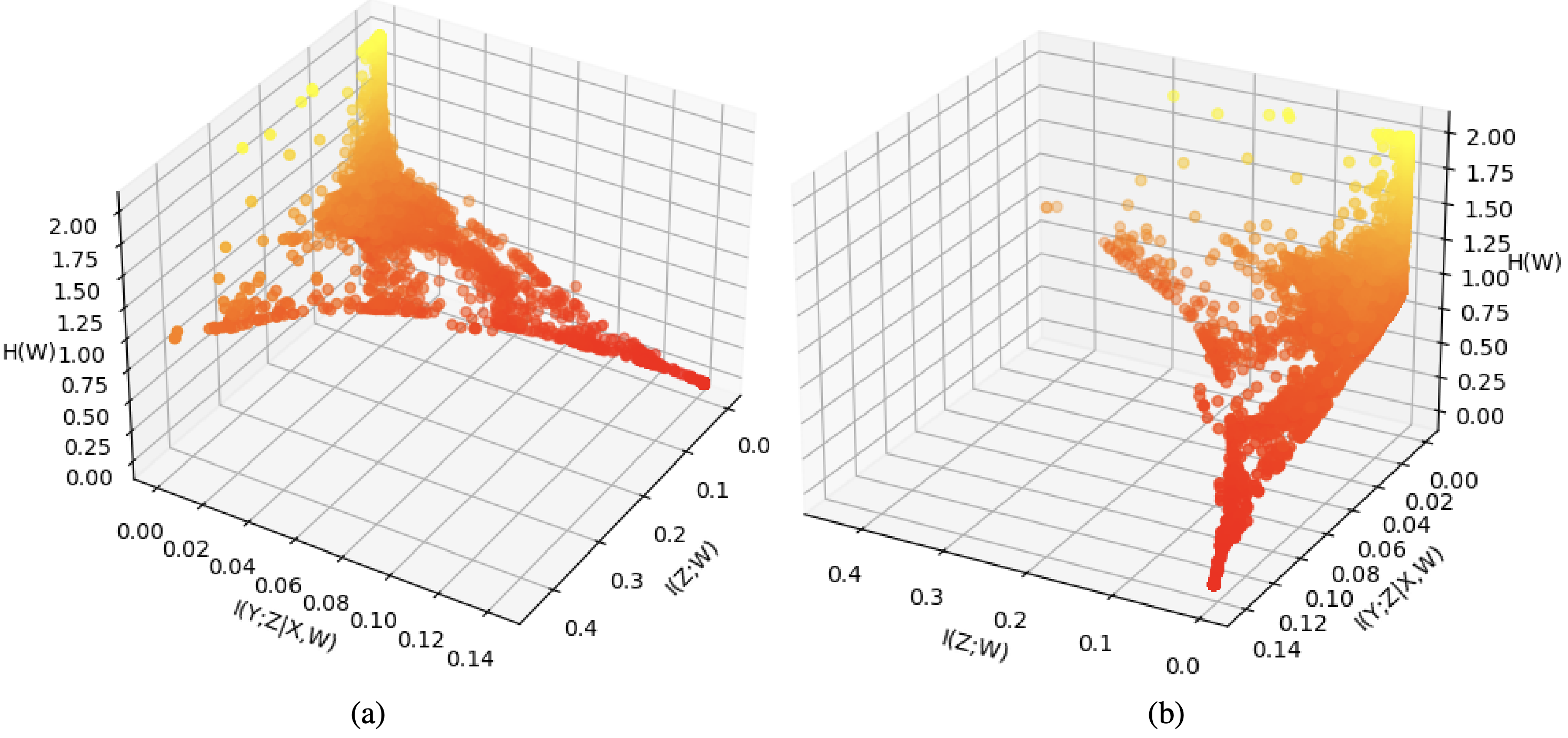
We proved that the IV LatentSearch finds the stationary point of the relaxed objective function. The approximated CCE can be obtained by setting a threshold for $I(Z;Y|X,W)$ and $I(W;Z)$ and find the minimum value of $H(W)$ while the mutual information below the threshold.
Partial Identification
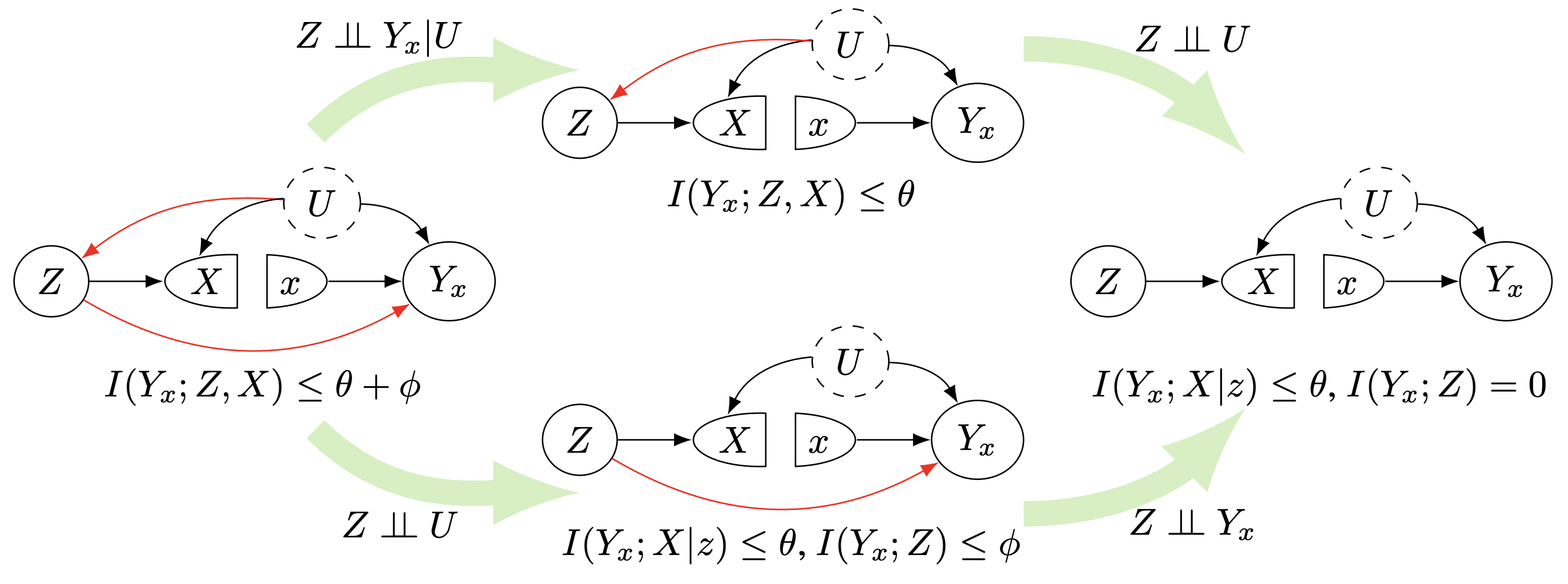
Assuming we know the upper bound of confounder’s entropy $H(U)\leq \theta$, we have the following Theorem for estimate the bounds of causal effect.
For variables $Z, X, Y$ with $|X|=n, |Y|=m$, and $|Z|=l$ and the compatible joint distribution $P(Z, X, Y)$. Assuming $CCE_{IV}(Z;Y|X,U) = \phi$. The causal effect of $x_t$ on $y_o$ is bounded by $\text{LB} \leq P(y_o|do(x_t)) \leq \text{UB}$, where $$ \begin{align*} &\text{LB}/\text{UB} = \min/\max{\left(\sum_{jl} b_{ojl}P(z_l)\right)}\\ &\text{subject to}\\ &P(z_k) b_{itk} = P(y_i, x_t, z_k); \forall i,k ; \sum_{ij}b_{ijk}=1; \forall k\\ & \sum_{i} b_{ijk} = P(x_j|z_k); \forall j,k; 0\leq b_{ijk}\leq 1 ; \forall i,j,k \\ & \sum_{ijk} b_{ijk}P(z_k)\log\left(\frac{b_{ijk}P(z_k) }{(\sum_{j’k’} b_{ij’k’}P(z_{k’}))(\sum_{i’} b_{i’jk}P(z_k))}\right) \leq \theta+\phi. \end{align*} $$ If the marginal exchangeability holds, we can replace the last inequality constraint with the following two: $$ \begin{align*} &\sum_{ij} b_{ijk} \log\left(\frac{ b_{ijk}}{(\sum_{j’} b_{ij’k})(\sum_{i’} b_{i’jk})}\right) \leq \theta ; \forall k, \\ &\sum_{ijk} b_{ijk}P(z_k) \log\left(\frac{\sum_{j’} b_{ij’k}}{(\sum_{j’k} b_{ij’k}P(z_k))}\right) \leq \phi. \\ \end{align*} $$
This theorem allow us to estimate bounds of causal effect under different cases as shown in the figure below.
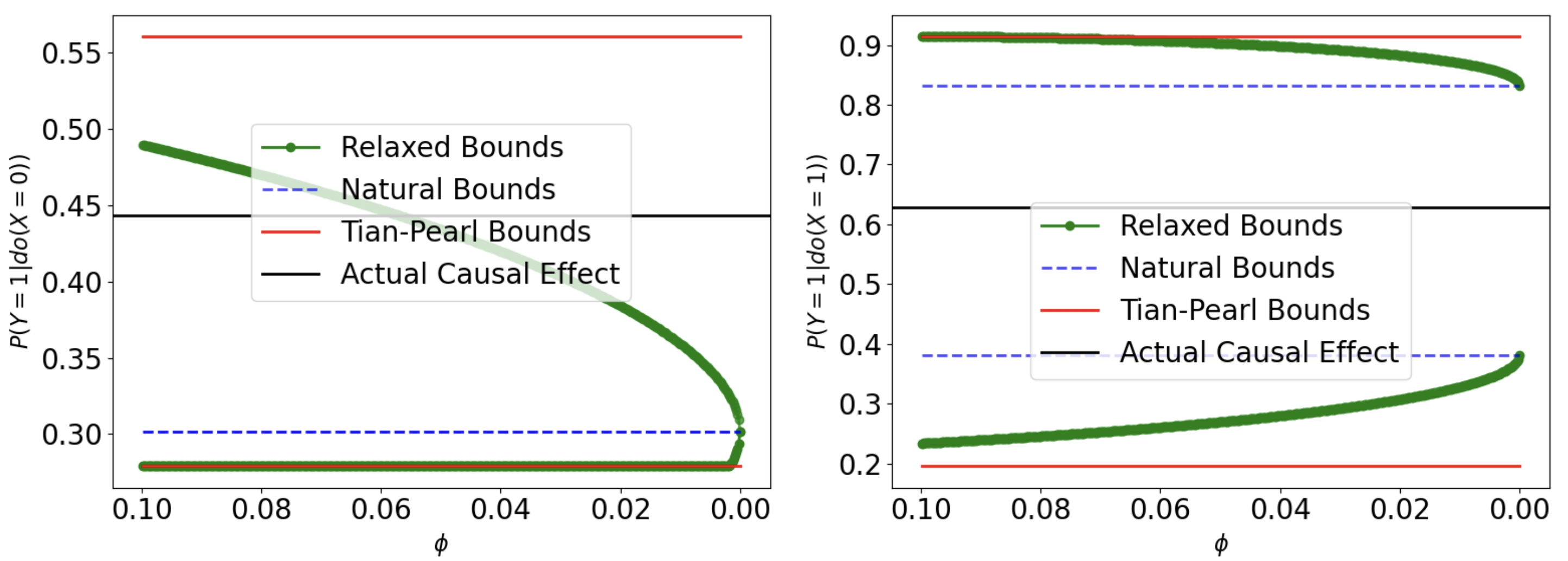
Here $\phi$ serves as a sensitivity parameter for the violation of IV assumption. The following plot shows an example of the affect of sensitivity parameter to the causal effect.
Falsify Invalid IV
As shown in the previous example, the CCE can be used to quantify the edge in a DAG. Assuming we know the upper bounds of confounder’s entropy, we can use this to check if a variable could satisfies the IV assumptions with the observed dataset. In our experiments, we show that CCE can be used to reject invalid IV effectively. And we show experimentally that when the entropy of confounder is unknown, it can be used to select the variable that is more likely to be the IV. For more detail about the experiments, please check our paper “Conditional Common Entropy for Instrumental Variable Testing and Partial Identification”.